IPTW and IPCW

The Marginal Structural Model (MSM) is a Cox-typed model, which is adjusted selection bias by inverse probability treatment weighting (IPTW) and inverse probability censoring weighting (IPCW). We introduce these two tools in this section.

Using the same notations (see Causal Inference 1 ), we can write the propensity score as . Then, the IPTW estimator for survival function is

is unbiased for .

However, in survival analysis, we also consider censoring. Note we fit the MSM under the assumption:

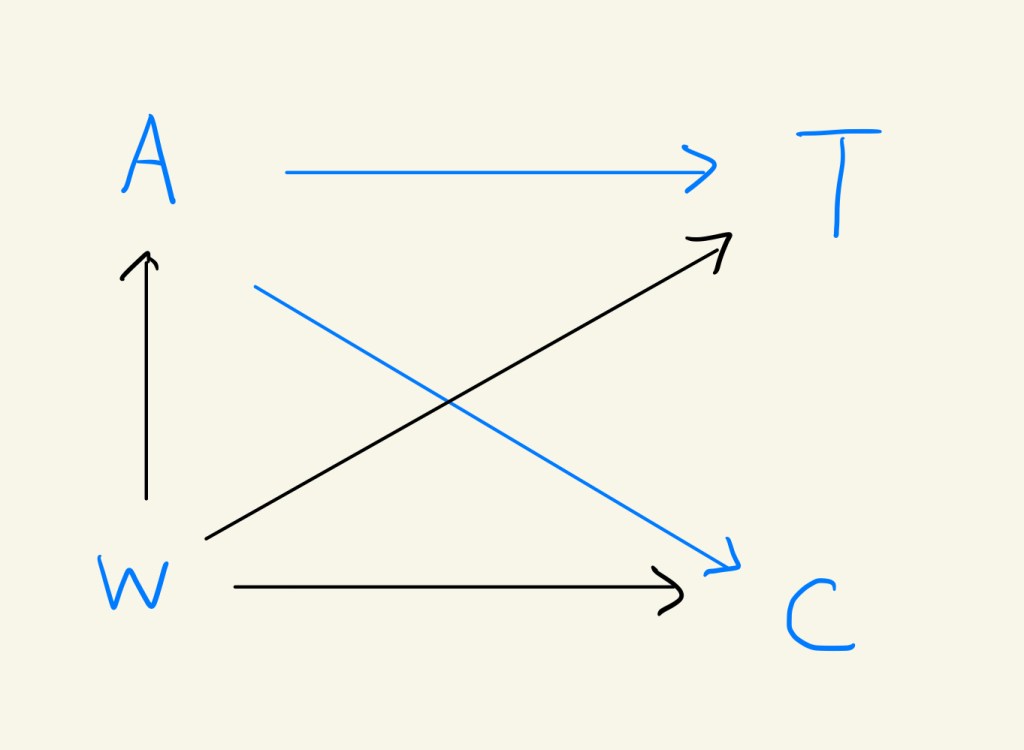
where C is the censoring time. In the above diagram, we know that censoring depends on confounders as well as treatment. To correct selection bias due to censoring, we need to model C against W, which is IPCW. Thus, let , the inverse weight is a product: .

Estimation for parameters

First, we discuss a simple case: point treatment. We consider the estimation for treatment effect under the assumption that patients remain on therapy once they start it. In this scenario, the Marginal structural Cox Model is

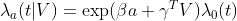
where is the conditional hazard function of given .

Then, the naive IPTW/IPCW weights should be

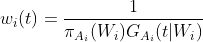
Furthermore, we have stabilized weights for numerical stability and statistical efficiency:

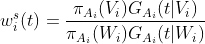
where and .

To formalize above, we go back to original setting. Consider treatment path: , our MSM is:

with assumptions

1. sequential exchangeability
2. the outcome depends on the treatment path only through the current treatment

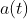
Let

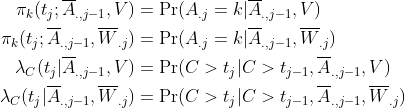
Then stabilized weights:

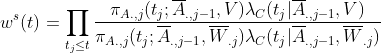
Finally, we estimate parameters by weighted partial-likelihood score:

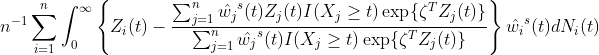
where , is observed on the ith subject, and .

Note that is consistency estimated by our IPTW/IPCW estimator, under the untestable assumption of no unmeasured confounders given the measured risk factors in W.

Implementation, Software and Dataset

The practical problem faced by the investigator is how to obtain the quantities of . To show the procedure, we first consider a special case. We want to estimate the causal effect of zidovudine on the survival of human immunodeficiency virus-positive men participating in the Multicenter AIDS Cohort Study. To obtain the estiamtion of IPTW weights, we need to estimate consistently and for each subject and time point. Because any subject starting zidovudine was assumed to remain on it thereafter, we can regard the time to starting zidovudine as a failure time variable and model the probability of starting zidovudine through a pooled logistic model that treat each person-month as an observation. For example, we can fit the model , and obtain estimates for the unknown parameters. Next, the estimated predicted values from this model are the estimated probabilities of subject i not starting zidovudine in month k given that zidovudine had not been started by month k-1. Our estimate of for person i in month k is the product

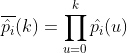
if subject i did not start zidovudine up to month k. Or, if subject i started zidovudine at month t, for t is not larger than k, the estimation is

Similarly, we can estimate in the same logistic model, except with the covariate W(k) removed from the model.

The third step in this case, we estimate IPCW weights in a manner analogous to the estimation of IPTW (which we already showed above) except with A(k) replaced by C(k) as the outcome variable. Then, by combining our estimations, we finally obtain IPTW/IPCW weights, which help us derive the MSM.

Next, we show an example for running MSM in R. We use R package (ipw) to estimate IPTW/IPCW weights, and put them into coxph. Please see the following example (we use another data, HAART, in ipw package):

Therefore, we can easily estimate the effect of treatment, and obtain the MSM output by R.

Last but not least, we want to discuss more details about dataset. If the data include censor, time-varying treatment, time-varying confounder, we can consider MSM to estimate causal effect of treatment on survival time. However, although MSM allows treatment to be frequently changed during the time goes on, the loading of calculation might be huge. In practical, because we estimate IPTW/IPCW weights for each subject and time point, the procedure is time consuming. That’s why our examples (zidovudine data and HAART data) assume that each patient remains the treatment once he/she receive the therapy.

Performance of MSM

We compare MSM to other three methods, which are introduced earlier than MSM by Robins and co-workers. These three methods are for estimation of the causal effect of a time-varying treatment in the presence of time-varying confounders: the parametric g-computation algorithm formula estimator, g-estimation of structural nested models (SNM), and the iterative conditional expectations (ICE) estimator. When

1. Both treatment and the confounders are discrete variables
2. They are measured at only a few time points
3. The study size is large

then estimation can be carried out using saturated models (nonparametrically), and all four methods are precisely equivalent. In contrast, they are different when one must introduce modeling assumptions for sparse multivariate data.

First, ICE estimators are rarely used, since they often lead to logically incompatible models and will not be discussed further. Also, the parametric g-computation algorithm estimator is quite difficult to determine whether one’s confidence interval for the treatment effect includes the null hypothesis (no effect). On the other hand, SNM and MSM are interpretable, because they include parameters that represent the null hypothesis of no treatment effect.

Second, MSM has 2 advantages over SNM: (1) logistic SNM cannot be conveniently used to estimate the effect of treatment of dichotomous (0,1) outcomes unless the outcome is rare. (2) MSM is a resemble standard model, whereas SNM do not.

Nevertheless, SNM has a number of advantages over MSM. For example, MSM should not be used to estimate effects in studies in which, at each time k there is a covariate level L(k) such that all subjects with that level of the covariate are certain to receive the identical exposure a(k).

In conclusion, although it is not easy to directly judge which of the four methods are the best, we should always choose the most appropriate method under different situations. In our purpose, we want to obtain a Cox-type model which is also interpretable, so we consider MSM to estimate the causal effect of treatment.