Interest Questions

A time-dependent confounder that is affected by previous treatment or confounders is a complicated problem in survival analysis. Because time-dependent Cox model may produce biased effect estimates under the exsistence of such confounders, we cannot use Cox model but need another method to solve the problem. For example, we want to estimate the causal effect of zidovudine on the survival of human immuno-deficiency virus-positive men. However, CD4 lymphocyte count is both a time-dependent confounder of the causal effect (zidovudine on survival) and is affected by past zidovudine treatment. The problem was already solved by introduced Marginal Structural Models (MSM). Because time-dependent confounders that are affected by previous treatment are usually observed in clinical trials or survival datasets, MSM definitely made a great contribution in causal inference for survival analysis.

Needed Random Variables

As we mentioned in the last section, we have the follwing random variables:

1. A(t): observed treatment /exposure at time t
2. W(t): possible confounders at time t
3. T: survival time

Our goal is to assess the causal effect of A on T, and adjust W simultaneously. In our example, A is zidovudine, W is CD4 count, and T is the survival time of virus-positive men.

Causal Effect

In MSM, we see causal hazard ratio instead of average treatment effect. We obtain causal hazard ratio by modeling conditional hazard function with adjustment to confounders. The benefit of modeling is to tell us more information about mortality risk with covariates. Notice that MSM allow us adjust for confounders without including them as covariates, because if we including confounders in our model, it will block the causal path between previous treatment and outcome. We will see more details about this in the next section. Now, we back to our interest causal effect. Here is our MSM:

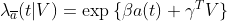
where is treatment path, and is the conditional hazard function given , which denotes baseline covariates that we want to adjust (e.g. gender, age, etc.). Note that .

Therefore, according to MSM, we know that is causal hazard ratio of treatment (a=1) adjusting for . Note that under sequential conditional exchangeability assumption, we can build stabilized weights. Then, we can estiamte our weighted partial-likelihood score. We will interpret more details in the next article.

Relationship Between Variables

We use a directed acyclic graph (DAG) to show the relationship:

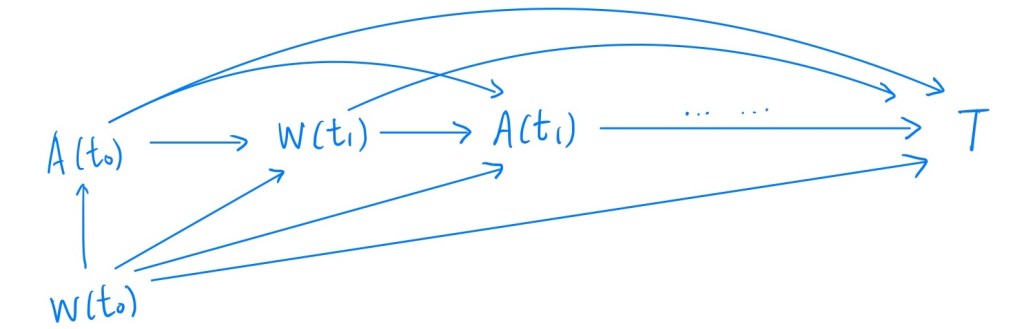
The DAG illlustrates the time-varying treatment in the presence of time-varying confounding. If we intervent any W in this graph, it will block the path between previous treatment and T; therefore, we need MSM.

Next, we will discuss how to identify interest causal effect : https://pkc-stat-888.com/2022/10/25/causal-inference-2-identification/

References

1. Robins, J. M., Hernan, M. A., & Brumback, B. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology, 11(5), 550-560.
2. Hernán, M. Á., Brumback, B., & Robins, J. M. (2000). Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology, 561-570.
3. Mao, L. Applied survival Analysis: From Univariate to Complex Time-to-Event Outcomes. (textbook for STAT 741)